Line Angle
Overview
This transform calculates the angle of a line at a specific position along its length for each point in time.
Detailed Description
The Line Angle transform provides a way to quantify the orientation of a line in a 2D space. This can be particularly useful for analyzing the movement or orientation of objects that are tracked as lines. The angle is measured relative to a customizable reference vector, which defaults to the positive x-axis (0 degrees).
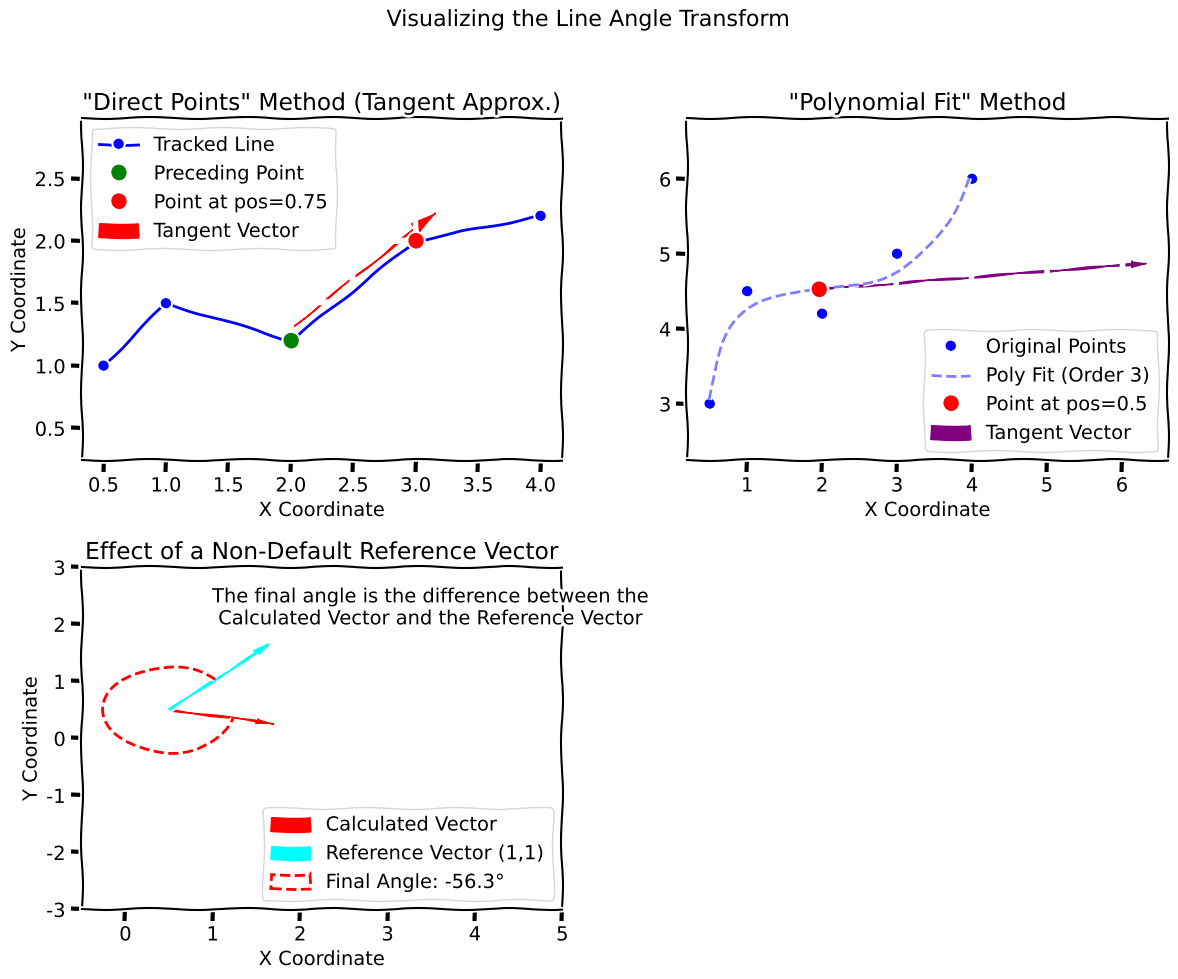
There are two methods for calculating the angle:
- Direct Points: This method approximates the tangent at a given
positionby calculating the angle of the vector between the point at that position and the point immediately preceding it. This is a simple and fast method suitable for getting a local orientation. - Polynomial Fit: This method fits a polynomial of a given order to the line’s points (parameterized by their cumulative distance). The angle is then calculated from the derivative of the polynomial at the specified
position. This method can provide a more accurate estimate of the tangent angle at a specific point along a curved line.
Neuroscience Use Cases
In neuroscience, this transform can be used to analyze a variety of data:
- Whisker Tracking: The angle of a tracked whisker relative to the animal’s head can be calculated to study sensory input and motor control.
- Limb Tracking: The angle of a limb segment (e.g., the forearm) can be calculated to analyze reaching movements or other motor behaviors.
- Tongue Tracking: The angle of the tongue during licking or other oral movements can be quantified.
Parameters
This transform has the following parameters:
position: A value between 0.0 and 1.0 that specifies the point along the line at which to calculate the angle. For example,0.5would be the midpoint of the line.method: The calculation method to use.Direct Points: (Default) Calculates the angle based on the vector from the start of the line to the point atposition.Polynomial Fit: Fits a polynomial to the line and calculates the angle from the derivative.
polynomial_order: The order of the polynomial to fit to the line when using thePolynomial Fitmethod. A higher order can capture more complex curves but requires more points and can be prone to overfitting. A typical value is 2 or 3.reference_x: The x-component of the reference vector. Defaults to1.0.reference_y: The y-component of the reference vector. Defaults to0.0. The default vector(1.0, 0.0)corresponds to the positive x-axis, meaning angles are measured with 0 degrees pointing to the right.
Example Configuration
Here is a complete example of a JSON configuration file that could be used to run this transformation. This example calculates the angle at the midpoint of a line using the “Direct Points” method.
[
{
"transformations": {
"metadata": {
"name": "Line Angle Pipeline",
"description": "Test line angle calculation on line data",
"version": "1.0"
},
"steps": [
{
"step_id": "1",
"transform_name": "Calculate Line Angle",
"phase": "analysis",
"input_key": "test_line",
"output_key": "line_angles",
"parameters": {
"position": 0.5,
"method": "Direct Points",
"polynomial_order": 3,
"reference_x": 1.0,
"reference_y": 0.0
}
}
]
}
}
]