Analog Hilbert Phase

Overview

This transform calculates the instantaneous phase of an analog signal, which is useful for analyzing oscillations.

Detailed Description

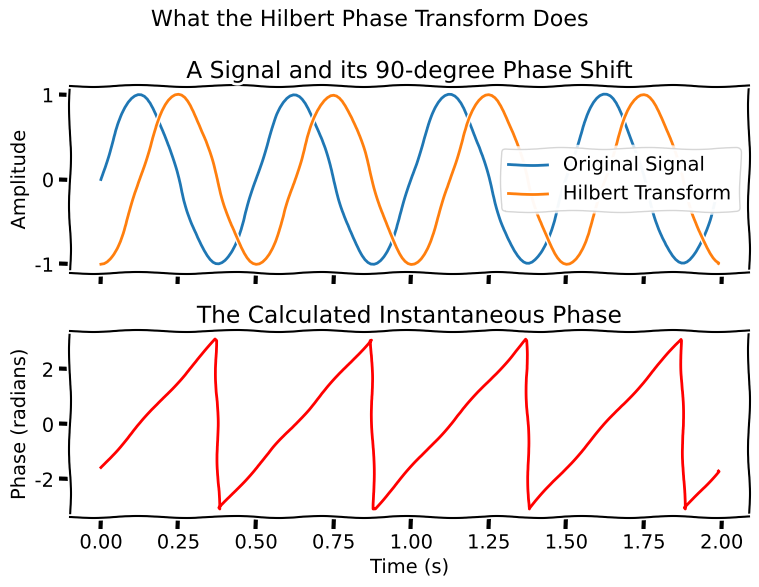
The Hilbert transform is a mathematical operation that shifts the phase of all positive frequency components of a signal by -90 degrees and all negative frequency components by +90 degrees. When this phase-shifted signal (the imaginary part) is combined with the original signal (the real part), it forms a complex-valued “analytic signal”.

The instantaneous phase is the angle of this complex number at each point in time. It provides a way to represent an oscillating signal in terms of its phase, which progresses from -π to +π for each cycle of the oscillation. This transform uses an efficient FFT-based method to compute the Hilbert transform.

Neuroscience Use Cases

In neuroscience, analyzing the phase of neural signals is crucial for understanding brain function. Some common applications include:

• Rhythmic Behaviors: The phase of signals from sensors tracking rhythmic behaviors like whisking, sniffing, or licking can be extracted to correlate them with neural activity.

Parameters

This transform has the following parameters:

• low_frequency: The low-cut frequency for the bandpass filter, in Hertz. This determines the lower end of the frequency range you want to analyze.
• high_frequency: The high-cut frequency for the bandpass filter, in Hertz. This determines the upper end of the frequency range you want to analyze.
• discontinuity_threshold: A time gap, in samples, above which the signal is considered to have a break. The transform will process the continuous segments separately. This is useful for data with missing samples or interruptions.

Example Configuration

Here is a complete example of a JSON configuration file that loads data and applies the Analog Hilbert Phase transform.

[
{
    "transformations": {
        "metadata": {
            "name": "Hilbert Phase Pipeline",
            "description": "Test Hilbert phase calculation on analog signal",
            "version": "1.0"
        },
        "steps": [
            {
                "step_id": "1",
                "transform_name": "Hilbert Phase",
                "phase": "analysis",
                "input_key": "test_signal",
                "output_key": "phase_signal",
                "parameters": {
                    "low_frequency": 5.0,
                    "high_frequency": 15.0,
                    "discontinuity_threshold": 1000
                }
            }
        ]
    }
}
]

References

Hill, D.N., Curtis, J.C., Moore, J.D., Kleinfeld, D., 2011. Primary motor cortex reports efferent control of vibrissa motion on multiple timescales. Neuron 72, 344–356. https://doi.org/10.1016/j.neuron.2011.09.020